Experimentos de Matemáticas

Dos teoremas con un triangulo de papel Introducción La Real Sociedad Matemática Española, fundada en 1911, tiene como objetivos la promoción y divulgación de la Matemática y sus aplicaciones, su enseñanza y el fomento de su investigación. Se presentaron en el stand actividades del proyecto «Ciencia en acción» de la RSME, RSEF y FECYT. Desarrollo Tomamos un triángulo cualquiera de papel y lo colocamos de manera que el lado mayor sea la base b. Marcamos su altura h (doblando como se indica en la figura 1). Llevando los tres vértices del triángulo al punto donde la altura corta a la base (figura 2), obtenemos un rectángulo (figura 3). Aplicación Hemos probado dos teoremas: Los tres ángulos del triángulo original suman 180º Observamos que tanto la altura como la base y el área de este rectángulo son la mitad que las del triángulo original (todo esto lo comprobamos al doblar).

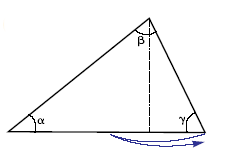Figura 1 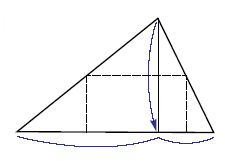Figura 2 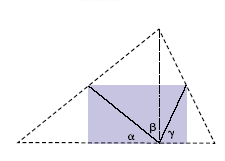Figura 3

	b · h		b · h
En consecuencia, el área del rectángulo es,		y la del triángulo,
Encuentra la estrategia y gana: juegos de nim Materiales: Dependiendo del juego de nim, se necesitarán un determinado número de cerillas (pueden valer también palillos, lápices, caramelos, etc.) y una mesa donde colocarlas. Fundamento científico Los juegos de nim se plantean a partir de una serie de filas (cuatro en el gráfico adjunto) con un número determinado de cerillas o palillos en cada una de ellas (1, 3, 5 y 7). Cada uno de los dos jugadores debe retirar en su turno de una sola fila una cerilla como mínimo, y hasta un máximo de todas las cerillas que queden. Gana el jugador que retira la última cerilla. Para el juego concreto mostrado en la figura, existe una estrategia que garantiza la victoria del segundo jugador. Esta estrategia se basa en la numeración en sistema binario, donde el uno se representa por «1», el dos por «10», el tres por «11», etc. Desarrollo (estrategia para el 2.º jugador) Escribe el número de cerillas que hay en cada fila, en sistema binario. Coloca estos números (escritos en binario) unos debajo de otros, ajustados por la derecha. Suma cada columna de cifras por separado en sistema decimal (como toda la vida). Observa que, inicialmente, todas las sumas de dichas columnas son pares (el cero es par). Cualquier movimiento del primer jugador destruye esta propiedad, puesto que al menos una de las columnas será un número impar. Tú deberás responder con un movimiento tal que dejes todas las columnas en número par. Mantén esta estrategia hasta que todas las columnas sean ceros, y ya has ganado. 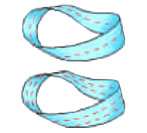La cinta de Möbius Materiales Tijeras Pegamento Lápices Tiras de papel Introducción En 1858, Möbius hizo un sorprendente descubrimiento: encontró una superficie de una sola cara y un solo borde con sorprendentes propiedades: la «banda de Möbius». Desarrollo Toma una tira de papel, haz una torsión y une los extremos de forma que puedas obtener la banda de la figura de la derecha. Ayudándote del lápiz dibuja una línea sobre ella recorriéndola en su totalidad. ¿Has cambiado de cara en tu recorrido? ¿Cuántas caras y cuántos bordes hay en tu banda? Construye dos bandas de Möbius y corta cada una como indica el dibujo de arriba, a 1/2 y a 1/3 del borde. ¿Qué has obtenido en cada caso? Comprueba que en esta banda se pueden resolver problemas que no tienen solución en un plano. Por ejemplo: «¿Se pueden unir tres casas con tres pozos con caminos que no se corten?».	4		2